- Un estudiante que realiza un examen debe responder 7 de las 10 preguntas. El orden no importa. ¿De cuántas formas puede responder el examen?
Existen10 10! 10.9.8 C7 = --- = ------ = 120 7!3! 3.2.1combinaciones posibles de preguntas que puede contestar. - Juan quiere dar una fiesta para algunos de sus amigos. Debido al tamaño de su casa, sólo puede invitar a 11 de sus 20 amigos. ¿De cuántas formas puede seleccionar a los invitados?
Hay20 20! C11 = ---- = 167.960 11!9!formas de elegir a los 11 amigos. - En una reunión de 6 personas, ¿cuántos saludos de mano pueden intercambiarse, si entre cada 2 personas, se dan la mano una sola vez?
6 6! 6.5 C2 = ---- = --- = 15 2!4! 2 - Una persona que sale de vacaciones desea llevarse 4 libros para leer: dispone de 4 novelas policiales y 6 libros de cuentos cortos. ¿De cuántas formas puede hacer la elección si quiere llevar al menos una novela?
6 N C C C --> 4C3 = 80 4 6 N N C C --> C2C2 = 90 4 N N N C --> C36 = 24 N N N N --> 1 80 + 90 + 24 + 1 = 195 - ¿Cuántos bytes contienen
- exactamente dos unos?
8 8! C2 = --- = 28 2!6! Ejemplo: 1 0 0 1 0 0 0 0 - exactamente cuatro unos?
8 8! C4 = --- = 70 4!4! Ejemplo: 0 1 0 1 0 1 1 0 - exactamente seis unos?
8 8! C2 = --- = 28 6!2! Ejemplo: 1 1 1 0 1 1 0 1 - al menos seis unos?
8 28 + C7 + 1 = 28 + 8 + 1 = 37 (Sumamos los bytes con 6 unos, los bytes con 7 unos y el byte con 8 unos) Ejemplo: 1 1 1 0 1 1 1 1
- exactamente dos unos?
Regla general de Conteo
lunes, 12 de diciembre de 2011
Ejemplos de regla de Combinaciones
Ejemplos de regla de permutaciones
- ¿Cuántas permutaciones existen para las ocho letras a,b,c,d,e,f,g,h?P8 = 8! = 40.320.
- ¿Cuántas de las permutaciones de (a) comienzan con la letra a?P7 = 7! = 5.040.
- ¿Cuántas de las permutaciones de (a) comienzan con la letra a y terminan con la letra c?P6 = 6! = 720.
- ¿Cuántas permutaciones existen para las ocho letras a,b,c,d,e,f,g,h?
- ¿De cuántas formas es posible ordenar los símbolos a,b,c,d,e,e,e,e,e de modo que ninguna e quede junto a otra?
e _ e _ e _ e _ e P4 = 4! = 24 - ¿De cuántas maneras se pueden colocar las letras de VISITING?Si consideramos que las tres I son distintas, podemos formar P8 palabras. Así, la permutación VI1SI2TI3NG sería distinta de VI2SI1TI3NG. Pero esto no es lo que queremos, en realidad no hay diferencia entre esas dos permutaciones. Como las tres I pueden ubicarse de P3 maneras, cada palabra se está repitiendo P3 veces. Por lo tanto hay
P8/P3 = 8!/3! = 6.720 disposiciones diferentes. - ¿Cuántas de ellas tienen las tres letras I juntas?
Las restantes 5 letras pueden ordenarse de P5 formas. Las 3 letras I pueden ubicarse en 6 posiciones diferentes: al principio, al final o en cualquiera de los 4 espacios entre las otras 5 letras. Así, hay6.5! = 6! = 720 palabras con las tres I juntas.III_ _ _ _ _ _III_ _ _ _ _ _III_ _ _ _ _ _III_ _ _ _ _ _III_ _ _ _ _ _IIIb) Suponga que se han nombrado como representantes del salón a Daniel como Presidente, a Arturo como secretario y a Rafael como tesorero, pero resulta que a alguien se le ocurre hacer algunos cambios, los que se muestran a continuación:CAMBIOS PRESIDENTE:Daniel Arturo Rafael Daniel
SECRETARIO:Arturo Daniel Daniel Rafael
TESORERO:Rafael Rafael Arturo Arturo
Ahora tenemos cuatro arreglos, ¿se trata de la misma representación?Creo que la respuesta sería no, ya que el cambio de función que se hace a los integrantes de la representación original hace que definitivamente cada una de las representaciones trabaje de manera diferente, ¿importa el orden de los elementos en los arreglos?. La respuesta definitivamente sería sí, luego entonces las representaciones antes definidas son diferentes ya que el orden o la forma en que se asignan las funciones sí importa, por lo tanto es este caso estamos tratando con permutaciones.A continuación obtendremos las fórmulas de permutaciones y de combinaciones, pero antes hay que definir lo que es n! (ene factorial), ya que está involucrado en las fórmulas que se obtendrán y usarán para la resolución de problemas.n!= al producto desde la unidad hasta el valor que ostenta n.n!= 1 x 2 x 3 x 4 x………..x nEjem.10!=1 x 2 x 3 x 4 x………x 10=3,628,8008!= 1 x 2 x 3 x 4 x………x 8=40,320 6!=1 x 2 x 3 x 4 x……….x 6=720, etc., etc.
Obtención de fórmula de permutaciones.Para hacer esto, partiremos de un ejemplo.¿Cuántas maneras hay de asignar los cuatro primeros lugares de un concurso de creatividad que se verifica en las instalaciones de nuestro instituto, si hay 14 participantes?Solución:Haciendo uso del principio multiplicativo,14×13×12×11 = 24,024 maneras de asignar los primeros tres lugares del concursoEsta solución se debe, a que al momento de asignar el primer lugar tenemos a 14 posibles candidatos, una vez asignado ese lugar nos quedan 13 posibles candidatos para el segundo lugar, luego tendríamos 12 candidatos posibles para el tercer lugar y por último tendríamos 11 candidatos posibles para el cuarto lugar.Luego si n es el total de participantes en el concurso y r es el número de participantes que van a ser premiados, y partiendo de la expresión anterior, entonces.14×13×12×11= n x (n - 1) x (n - 2) x ………. x (n – r + 1)si la expresión anterior es multiplicada por (n – r)! / (n – r)!, entonces= n x (n –1 ) x (n – 2) x ……… x (n – r + 1) (n – r)! / (n – r)!= n!/ (n – r)!Por tanto, la fórmula de permutaciones de r objetos tomados de entre n objetos es:Esta fórmula nos permitirá obtener todos aquellos arreglos en donde el orden es importante y solo se usen parte ® de los n objetos con que se cuenta, además hay que hacer notar que no se pueden repetir objetos dentro del arreglo, esto es, los n objetos son todos diferentes.Entonces, ¿ qué fórmula hay que usar para arreglos en donde se utilicen los n objetos con que se cuenta?Si en la fórmula anterior se sustituye n en lugar de r, entonces.nPn= n!/ (n –n)! = n! / 0! = n! / 1 = n!
Como 0! = 1 de acuerdo a demostración matemática, entoncesnPn= n!
- ¿De cuántas maneras se pueden colocar las letras de VISITING?
Ejemplos de regla de conteo
- ¿Cuántas palabras de tres letras se pueden formar con cinco consonantes y tres vocales de modo que cada palabra comience y termine en consonante?
C V C --- --- --- 5.3.4 = 60 (regla del producto) 5 3 4 - Determine el número de enteros de seis dígitos (que no comiencen con cero) en los que
- ningún dígito se pueda repetir.
9 9 8 7 6 5 --- --- --- --- --- --- 9.9.8.7.6.5 = 136.080 (regla del producto) - se pueden repetir los dígitos.
9.10.10.10.10.10 = 900.000 (regla del producto)
- ningún dígito se pueda repetir.
- Ana y María vieron a dos hombres alejarse en automóvil frente a una joyería, justo antes de que sonara una alarma contra robos. Cuando fueron interrogadas por la policía, las dos jóvenes dieron la siguiente información acerca de la placa (que constaba de dos letras seguidas de cuatro dígitos). María estaba segura de que la segunda letra de la placa era una O o una Q, y que el último dígito era un 3 o un 8. Ana dijo que la primera letra de la placa era una C o una G y que el primer dígito era definitivamente un 7.
¿Cuántas placas diferentes tendrá que verificar la policía?
C/G Q/O 7 0 a 9 0 a 9 8 ó 3 ----- ----- ----- ----- ----- ----- | | | | | | 2 x 2 x 1 x 10 x 10 x 2 = 800 (regla del producto) - Tres pueblos, designados como A, B y C, están intercomunicados por un sistema de carreteras de doble sentido.
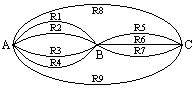
- ¿De cuántas formas puede Juan ir del pueblo A al pueblo C?2 + 4.3 = 14 (reglas de la suma y del producto)
- ¿Cuántos trayectos puede hacer Juan del pueblo A al pueblo C y de regreso al pueblo A?14.14 = 196 (regla del producto)
- ¿Cuántos de los trayectos completos de la parte (b) son tales que el viaje de regreso (del pueblo C al pueblo A) es diferente, al menos parcialmente, de la ruta que toma Juan del pueblo A al pueblo C? (Por ejemplo, si Juan viaja de A a C por las rutas R1 y R6 podría regresar por las rutas R6 y R2, pero no por R1 y R6).14.13 = 182 (regla del producto)
- ¿De cuántas formas puede Juan ir del pueblo A al pueblo C?
Combinaciones
La Técnica de la Combinación
En una permutación, el orden de los objetos de cada posible resultado es diferente. Si el orden de los objetos no es importante, cada uno de estos resultados se denomina combinación. Por ejemplo, si se quiere formar un equipo de trabajo formado por 2 personas seleccionadas de un grupo de tres (A, B y C). Si en el equipo hay dos funciones diferentes, entonces si importa el orden, los resultados serán permutaciones. Por el contrario si en el equipo no hay funciones definidas, entonces no importa el orden y los resultados serán combinaciones. Los resultados en ambos casos son los siguientes:
Permutaciones: AB, AC, BA, CA, BC, CB
Combinaciones: AB, AC, BC
Combinaciones: Es el número de formas de seleccionar r objetos de un grupo de n objetos sin importar el orden.
La fórmula de combinaciones es:
n C r = n!
r! (n – r )!
Ejemplo:
En una compañía se quiere establecer un código de colores para identificar cada una de las 42 partes de un producto. Se quiere marcar con 3 colores de un total de 7 cada una de las partes, de tal suerte que cada una tenga una combinación de 3 colores diferentes. ¿Será adecuado este código de colores para identificar las 42 partes del producto?
Usando la fórmula de combinaciones:
n C r = n! = 7! = 7! = 35
r! (n – r )! 3! ( 7 – 3 )! 3! 4!
El tomar tres colores de 7 posibles no es suficiente para identificar las 42 partes del producto.
Permutaciones
La Técnica de la Permutación
Como vimos anteriormente la técnica de la multiplicación es aplicada para encontrar el número posible de arreglos para dos o más grupos. La técnica de la permutación es aplicada para encontrar el número posible de arreglos donde hay solo u grupo de objetos. Como ilustración analizaremos el siguiente problema: Tres componentes electrónicos - un transistor, un capacitor, y un diodo - serán ensamblados en una tablilla de una televisión. Los componentes pueden ser ensamblados en cualquier orden. ¿De cuantas diferentes maneras pueden ser ensamblados los tres componentes?
Las diferentes maneras de ensamblar los componentes son llamadas permutaciones, y son las siguientes:
T D C D T C C D T
T C D D C T C T D
Permutación: Todos los arreglos de r objetos seleccionados de n objetos posibles
La fórmula empleada para contar el número total de diferentes permutaciones es:
n P r = n!
(n – r )!
Donde:
nPr es el número de permutaciones posible
n es el número total de objetos
r es el número de objetos utilizados en un mismo momento
n P r = n! = 3! = 3 x 2 = 6
(n – r )! ( 3 – 3 )! 1
Ejemplo:
Suponga que hay ocho tipos de computadora pero solo tres espacios disponibles para exhibirlas en la tienda de computadoras. ¿De cuantas maneras diferentes pueden ser arregladas las 8 máquinas en los tres espacios disponibles?
n P r = n! = 8! = 8! = 336
(n – r )! ( 8 – 3 )! 5!
En el análisis anterior los arreglos no presentan repeticiones, es decir, no hay dos espacios disponibles con el mismo tipo de computadora. Si en los arreglos se permite la repetición, la fórmula de permutaciones es la siguiente:
n Pr = nr
Para ilustrar el punto, queremos saber ¿cuántas series de 2 letras se pueden formar con las letras A, B, C, si se permite la repetición? Las permutaciones son las siguientes:
AA, AB, AC, BA, CA, BB, BC, CB, CC
Usando la fórmula:
n Pr = nr = 3P2 = 32 = 9
Reglas de conteo
Muchos problemas de conteo requieren una a la lista de todas las posibilidades, y contar con ellos. A veces ayuda a dibujar un árbol a la lista de todas las posibilidades. Muchos de los problemas sólo se pueden tratar con métodos ad hoc. Sin embargo, hay dos técnicas o reglas que se usan comúnmente en forma individual o dentro de los métodos más complicados. Vamos a ilustrar esto con un buffet de postres que tiene crema de nuez de helado de vainilla y la mantequilla y tarta de manzana, cerezas y arándanos.
Ejercicio: John tiene tres pares de pantalones, dos camisas de cuello alto, cinco camisas con cuellos, corbatas y cuatro. ¿Cuántos equipos tiene?
O (Además)
Si usted va a tomar un helado o pastel de postre, hay dos opciones (vainilla o nuez de mantequilla) si ha helado, y tres opciones (manzana, cereza, arándano o) si tiene pie. Por lo tanto hay 2 + 3 = 5 opciones para el postre. Si usted va a elegir una categoría o las anteras, a continuación, agregar el número de opciones en cada categoría. Esta es la regla de la suma de u.Y (multiplicación)
Algunas personas creen en el pastel a la mode, lo que implica pastel con helado en la parte superior, es decir, uno debe escoger un sabor de pastel y un sabor de helado. Uno puede enumerar las posibilidades: de manzana con vainilla, manzana con mantequilla de nuez, cereza con vainilla, cereza con nuez de mantequilla, arándanos con vainilla, arándano con nuez de mantequilla, y contar que hay seis posibilidades. O se puede observar que primero hay que elegir un sabor de pastel y luego elija un sabor de helado: 3 x 2 = 6. Cuando uno tiene que hacer una elección de una categoría y una selección de otra categoría, se multiplica el número de opciones en las dos categorías. Esta es la regla de la multiplicación y.Para que no pensemos que los problemas de conteo son triviales, considere un buffetwhich postre más grandes, además de vainilla y nuez de mantequilla y helado de manzana, alegre, y pastel de arándanos, también tiene chocolate, limón, frambuesa y queso con fresa. El buffet es supervisado por un nutricionista que insiste en que se comen pastel con helado, tarta de queso, pero se come solo. Por lo tanto usted debe elegir el pastel de queso o tarta a la mode, que se puede escribir con paréntesis como el pastel de queso o (tarta y helado).de las reglas anteriores o con la identificación y + y con x, esto se convierte en 4 + (3 x 2) = 10 postres Posible.Ejercicio: John tiene tres pares de pantalones, dos camisas de cuello alto, cinco camisas con cuellos, corbatas y cuatro. ¿Cuántos equipos tiene?
Poder regla
La regla de la multiplicación se extiende a más de dos opciones. Por ejemplo, el número de diferentes combinaciones de número tres son posibles para una cerradura de combinación con los números del 0 al 39? Hay 40 opciones para el primer número, cuarenta y opciones para el segundo número, y cuarenta y opciones para el tercer número. Tenga en cuenta que usted debe elegir un primer número y un número de segundos y un tercer número. Y los medios se multiplican, por lo que son 40 × 40 × 40 = 64.000 combinaciones posibles.Técnicas de conteo
Técnicas de Conteo
Si el número de posibles resultados de un experimento es pequeño, es relativamente fácil listar y contar todos los posibles resultados. Al tirar un dado, por ejemplo, hay seis posibles resultados.
Si, sin embargo, hay un gran número de posibles resultados tales como el número de niños y niñas por familias con cinco hijos, sería tedioso listar y contar todas las posibilidades.
Las posibilidades serían, 5 niños, 4 niños y 1 niña, 3 niños y 2 niñas, 2 niños y 3 niñas, etc. Para facilitar el conteo examinaremos tres técnicas: La técnica de la multiplicación, la técnica de la permutación, y la técnica de la combinación.
La Técnica de la Multiplicación
La técnica de la multiplicación: Si hay m formas de hacer una cosa y hay n formas de hacer otra cosa, hay m x n formas da hacer ambas cosas
En términos de fórmula
Número total de arreglos = m x n
Esto puede ser extendido a más de dos eventos. Para tres eventos, m, n, y o:
Número total de arreglos = m x n x o
Ejemplo:
Un vendedor de autos quiere presentar a sus clientes todas las diferentes opciones con que cuenta: auto convertible, auto de 2 puertas y auto de 4 puertas, cualquiera de ellos con rines deportivos o estándar. ¿Cuántos diferentes arreglos de autos y rines puede ofrecer el vendedor?
Para solucionar el problema podemos emplear la técnica de la multiplicación, (donde m es número de modelos y n es el número de tipos de rin).
Número total de arreglos = 3 x 2
No fue difícil de listar y contar todos los posibles arreglos de modelos de autos y rines en este ejemplo. Suponga, sin embargo, que el vendedor tiene para ofrecer ocho modelos de auto y seis tipos de rines. Sería tedioso hacer un dibujo con todas las posibilidades. Aplicando la técnica de la multiplicación fácilmente realizamos el cálculo:
Número total de arreglos = m x n = 8 x 6 = 48
Suscribirse a:
Entradas (Atom)